riemannien

riemannien

riemannien, ienne [ rimanjɛ̃, jɛn ] adj.
• 1903; de Bernhard Riemann (1826-1866)
♦ Math. Propre à Riemann et à ses théories mathématiques. Géométrie riemannienne, une des géométries non euclidiennes.

● riemannien, riemannienne adjectif Relatif aux théories de Bernhard Riemann.

⇒RIEMANNIEN, -IENNE, adj. et subst.
MATHÉMATIQUES
I. — Adj. Propre au mathématicien allemand Riemann et à ses théories. Espace riemannien; hypothèse, surface riemannienne. Helmholtz et Klein contribuèrent efficacement à la diffusion des conceptions riemanniennes et (...) les géométries à n dimensions furent de plus en plus largement utilisées (Hist. gén. sc., t. 3, vol. 1, 1961, p. 40).
♦ Géométrie riemannienne. ,,Géométrie fondée sur un système d'axiomes dans lequel le cinquième postulat d'Euclide est remplacé par un axiome exigeant que par un point extérieur à une droite on ne puisse mener aucune parallèle à cette droite`` (BOUVIER-GEORGE Math. 1979). La géométrie riemannienne est (...) une généralisation de la géométrie élémentaire ou euclidienne (CARTAN, Parallélisme abs., 1932, p. 4).
II. — Subst. Mathématicien travaillant suivant les théories de Riemann. Aux yeux des riemanniens la prétendue preuve des euclidiens se réduirait à l'affirmation, évidemment fausse, qu'un volume fini est infini parce qu'on peut y accumuler en nombre toujours plus grand des solides élémentaires tendant vers zéro (Gds cour. pensée math., 1948, p. 151).
Prononc.:[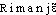], fém. [-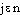]. Étymol. et Hist. 1. 1911 adj. « fondé sur les théories de Riemann » (H. POINCARÉ, Hyp. cosmogon., p. 254); 2. 1924 géométrie riemannienne (J. Phys. et Radium, p. 122D). Dér. du n. du mathématicien all. B. Riemann [1826-1866]; suff. -ien.

riemannien, ienne [ʀimanjɛ̃, jɛn] adj.
ÉTYM. Fin XIXe (30 mars 1903, in Rev. gén. des sc. no 6, p. 334); du nom du mathématicien Riemann (1826-1866).
❖
♦ Math. Propre à Riemann et à ses théories mathématiques. || Géométrie riemannienne : une des géométries non-euclidiennes (→ Parallèle, cit. 2). || Espace riemannien. || Surfaces riemanniennes.

Encyclopédie Universelle. 2012.

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Fibre vectoriel riemannien — Fibré vectoriel riemannien Un fibré vectoriel riemannien est la donnée d une métrique riemannienne sur un fibré vectoriel. Portail des mathématiques Ce document provient de « Fibr%C3%A9 vectoriel riemannien ». Catégorie : Géométrie riemannienne …   Wikipédia en Français

  • Fibré Vectoriel Riemannien — Un fibré vectoriel riemannien est la donnée d une métrique riemannienne sur un fibré vectoriel. Portail des mathématiques Ce document provient de « Fibr%C3%A9 vectoriel riemannien ». Catégorie : Géométrie riemannienne …   Wikipédia en Français

  • Fibré vectoriel riemannien — Un fibré vectoriel riemannien est la donnée d une métrique riemannienne sur un fibré vectoriel. Portail des mathématiques Ce document provient de « Fibr%C3%A9 vectoriel riemannien ». Catégorie : Géométrie riemannienne …   Wikipédia en Français

  • espace riemannien — Rymano erdvė statusas T sritis fizika atitikmenys: angl. Riemannian space vok. Riemann Raum, m rus. риманово пространство, n pranc. espace de Riemann, m; espace riemannien, m …   Fizikos terminų žodynas

  • continuum riemannien — Rymano kontinuumas statusas T sritis fizika atitikmenys: angl. Riemannian continuum vok. Riemannsches Kontinuum, n rus. риманов континуум, m pranc. continuum riemannien, m …   Fizikos terminų žodynas

  • nnien — riemannien …   Dictionnaire des rimes

  • riemannienne — ● riemannien, riemannienne adjectif Relatif aux théories de Bernhard Riemann …   Encyclopédie Universelle

  • Lexique de la géométrie riemannienne — La géométrie riemannienne est un domaine des mathématiques étudiant les propriétés des variétés riemanniennes. Cette page rappelle brièvement les définitions des termes récurrents rencontrés. Sommaire : Haut A B C D E F G H I J K L M N O P Q …   Wikipédia en Français

  • Espace symétrique — En mathématiques, et plus spécifiquement en géométrie différentielle, un espace riemannien symétrique est une variété riemannienne qui, en chaque point, admet une isométrie involutive dont ce point est un point fixe isolé. Plus généralement, un… …   Wikipédia en Français

  • Einbettungssatz von Nash — Der Einbettungssatz von Nash (nach John Forbes Nash Jr.) ist ein Ergebnis aus dem mathematischen Teilgebiet der riemannschen Geometrie. Er besagt, dass jede riemannsche Mannigfaltigkeit isometrisch in einen euklidischen Raum für ein geeignetes n… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”